ROBOT CONTROL JACOBIANS, VELOCITY, AND FORCE
Jacobian matrices are a super useful tool, and heavily used throughout robotics and control theory. Basically, a Jacobian defines the dynamic relationship between two different representations of a system. For example, if we have a 2-link robotic arm, there are two obvious ways to describe its current position: 1) the end-effector position and orientation (which we will denote 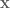 ), and 2) as the set of joint angles (which we will denote
), and 2) as the set of joint angles (which we will denote  ). The Jacobian for this system relates how movement of the elements of
). The Jacobian for this system relates how movement of the elements of  causes movement of the elements of
causes movement of the elements of 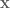 . You can think of a Jacobian as a transform matrix for velocity.
. You can think of a Jacobian as a transform matrix for velocity.
Formally, a Jacobian is a set of partial differential equations:
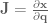 .
With a bit of manipulation we can get a neat result:
.
With a bit of manipulation we can get a neat result:
 ,
or
,
or
 ,
where
,
where  and
and  represent the time derivatives of
represent the time derivatives of 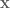 and
and  . This tells us that the end-effector velocity is equal to the Jacobian,
. This tells us that the end-effector velocity is equal to the Jacobian,  , multiplied by the joint angle velocity.
, multiplied by the joint angle velocity.
Why is this important? Well, this goes back to our desire to control in operational (or task) space. We’re interested in planning a trajectory in a different space than the one that we can control directly. Iin our robot arm, control is effected through a set of motors that apply torque to the joint angles, BUT what we’d like is to plan our trajectory in terms of end-effector position (and possibly orientation), generating control signals in terms of forces to apply in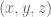 space. Jacobians allow us a direct way to calculate what the control signal is in the space that we control (torques), given a control signal in one we don’t (end-effector forces). The above equivalence is a first step along the path to operational space control. As just mentioned, though, what we’re really interested in isn’t relating velocities, but forces. How can we do this?
space. Jacobians allow us a direct way to calculate what the control signal is in the space that we control (torques), given a control signal in one we don’t (end-effector forces). The above equivalence is a first step along the path to operational space control. As just mentioned, though, what we’re really interested in isn’t relating velocities, but forces. How can we do this?
Energy equivalence and Jacobians
Conservation of energy is a property of all physical systems where the amount of energy expended is the same no matter how the system in question is being represented. The planar two-link robot arm shown below will be used for illustration.
Let the joint angle positions be denoted![\textbf{q} = [q_0, q_1]^T \textbf{q} = [q_0, q_1]^T](https://s0.wp.com/latex.php?latex=%5Ctextbf%7Bq%7D+%3D+%5Bq_0%2C+q_1%5D%5ET&bg=ffffff&fg=555555&s=0) , and end-effector position be denoted
, and end-effector position be denoted ![\textbf{x} = [x, y, 0]^T \textbf{x} = [x, y, 0]^T](https://s0.wp.com/latex.php?latex=%5Ctextbf%7Bx%7D+%3D+%5Bx%2C+y%2C+0%5D%5ET&bg=ffffff&fg=555555&s=0) .
.
Work is the application of force over a distance
 where
where 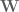 is work,
is work, 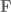 is force, and
is force, and  is velocity.
is velocity.
Power is the rate at which work is performed
 where
where 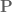 is power.
is power.
Substituting in the equation for work into the equation for power gives:
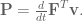 Because of energy equivalence, work is performed at the same rate regardless of the characterization of the system. Rewriting this terms of end-effector space gives:
Because of energy equivalence, work is performed at the same rate regardless of the characterization of the system. Rewriting this terms of end-effector space gives:
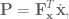 where
where 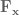 is the force applied to the hand, and
is the force applied to the hand, and  is the velocity of the hand. Rewriting the above in terms of joint-space gives:
is the velocity of the hand. Rewriting the above in terms of joint-space gives:
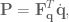 where
where  is the torque applied to the joints, and
is the torque applied to the joints, and  is the angular velocity of the joints. Setting these two equations (in end-effector and joint space) equal to each other and substituting in our equation for the Jacobian gives:
is the angular velocity of the joints. Setting these two equations (in end-effector and joint space) equal to each other and substituting in our equation for the Jacobian gives:
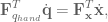
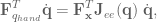
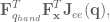
 where
where 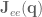 is the Jacobian for the end-effector of the robot, and
is the Jacobian for the end-effector of the robot, and 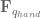 represents the forces in joint-space that affect movement of the hand. This says that not only does the Jacobian relate velocity from one state-space representation to another, it can also be used to calculate what the forces in joint space should be to effect a desired set of forces in end-effector space.
represents the forces in joint-space that affect movement of the hand. This says that not only does the Jacobian relate velocity from one state-space representation to another, it can also be used to calculate what the forces in joint space should be to effect a desired set of forces in end-effector space.
Building the Jacobian
First, we need to define the relationship between the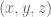 position of the end-effector and the robot’s joint angles,
position of the end-effector and the robot’s joint angles, 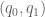 . However will we do it? Well, we know the distances from the shoulder to the elbow, and elbow to the wrist, as well as the joint angles, and we’re interested in finding out where the end-effector is relative to a base coordinate frame…OH MAYBE we should use those forward transformation matrices from the previous post. Let’s do it!
. However will we do it? Well, we know the distances from the shoulder to the elbow, and elbow to the wrist, as well as the joint angles, and we’re interested in finding out where the end-effector is relative to a base coordinate frame…OH MAYBE we should use those forward transformation matrices from the previous post. Let’s do it!
The forward transformation matrix
Recall that transformation matrices allow a given point to be transformed between different reference frames. In this case, the position of the end-effector relative to the second joint of the robot arm is known, but where it is relative to the base reference frame (the first joint reference frame in this case) is of interest. This means that only one transformation matrix is needed, transforming from the reference frame attached to the second joint back to the base.
The rotation part of this matrix is straight-forward to define, as in the previous section:
![\textbf{R}^1_0 = \left[ \begin{array}{ccc} cos(q_0) & -sin(q_0) & 0 \\ sin(q_0) & cos(q_0) & 0 \\ 0 & 0 & 1 \end{array} \right]. \textbf{R}^1_0 = \left[ \begin{array}{ccc} cos(q_0) & -sin(q_0) & 0 \\ sin(q_0) & cos(q_0) & 0 \\ 0 & 0 & 1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BR%7D%5E1_0+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+cos%28q_0%29+%26+-sin%28q_0%29+%26+0+%5C%5C+sin%28q_0%29+%26+cos%28q_0%29+%26+0+%5C%5C+0+%26+0+%26+1+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) The translation part of the transformation matrices is a little different than before because reference frame 1 changes as a function of the angle of the previous joint’s angles. From trigonometry, given a vector of length
The translation part of the transformation matrices is a little different than before because reference frame 1 changes as a function of the angle of the previous joint’s angles. From trigonometry, given a vector of length  and an angle
and an angle  the
the  position of the end point is defined
position of the end point is defined 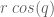 , and the
, and the  position is
position is  . The arm is operating in the
. The arm is operating in the  plane, so the
plane, so the  position will always be 0.
position will always be 0.
Using this knowledge, the translation part of the transformation matrix is defined:
![\textbf{D}^1_0 = \left[ \begin{array}{c} L_0 cos(q_0) \\ L_0 sin(q_0) \\ 0 \end{array} \right]. \textbf{D}^1_0 = \left[ \begin{array}{c} L_0 cos(q_0) \\ L_0 sin(q_0) \\ 0 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BD%7D%5E1_0+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+L_0+cos%28q_0%29+%5C%5C+L_0+sin%28q_0%29+%5C%5C+0+%5Cend%7Barray%7D+%5Cright%5D.+&bg=ffffff&fg=555555&s=0) Giving the forward transformation matrix:
Giving the forward transformation matrix:
![\textbf{T}^1_0 = \left[ \begin{array}{cc} \textbf{R}^1_0 & \textbf{D}^1_0 \\ \textbf{0} & \textbf{1} \end{array} \right] = \left[ \begin{array}{cccc} cos(q_0) & -sin(q_0) & 0 & L_0 cos(q_0) \\ sin(q_0) & cos(q_0) & 0 & L_0 sin(q_0)\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right], \textbf{T}^1_0 = \left[ \begin{array}{cc} \textbf{R}^1_0 & \textbf{D}^1_0 \\ \textbf{0} & \textbf{1} \end{array} \right] = \left[ \begin{array}{cccc} cos(q_0) & -sin(q_0) & 0 & L_0 cos(q_0) \\ sin(q_0) & cos(q_0) & 0 & L_0 sin(q_0)\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right],](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BT%7D%5E1_0+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+%5Ctextbf%7BR%7D%5E1_0+%26+%5Ctextbf%7BD%7D%5E1_0+%5C%5C+%5Ctextbf%7B0%7D+%26+%5Ctextbf%7B1%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcccc%7D+cos%28q_0%29+%26+-sin%28q_0%29+%26+0+%26+L_0+cos%28q_0%29+%5C%5C+sin%28q_0%29+%26+cos%28q_0%29+%26+0+%26+L_0+sin%28q_0%29%5C%5C+0+%26+0+%26+1+%26+0+%5C%5C+0+%26+0+%26+0+%26+1+%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0) which transforms a point from reference frame 1 (elbow joint) to reference frame 0 (shoulder joint / base).
which transforms a point from reference frame 1 (elbow joint) to reference frame 0 (shoulder joint / base).
The point of interest is the end-effector which is defined in reference frame 1 as a function of joint angle, and the length of second arm segment,
and the length of second arm segment,  :
:
![\textbf{x} = \left[ \begin{array}{c} L_1 cos(q_1) \\ L_1 sin(q_1) \\ 0 \\ 1 \end{array} \right]. \textbf{x} = \left[ \begin{array}{c} L_1 cos(q_1) \\ L_1 sin(q_1) \\ 0 \\ 1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7Bx%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+L_1+cos%28q_1%29+%5C%5C+L_1+sin%28q_1%29+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D.+&bg=ffffff&fg=555555&s=0) To find the position of our end-effector in terms of the origin reference frame multiply the point
To find the position of our end-effector in terms of the origin reference frame multiply the point 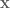 by the transformation
by the transformation  :
:
![\textbf{T}^1_0 \; \textbf{x} = \left[ \begin{array}{cccc} cos(q_0) & -sin(q_0) & 0 & L_0 cos(q_0) \\ sin(q_0) & cos(q_0) & 0 & L_0 sin(q_0)\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \; \left[ \begin{array}{c} L_1 cos(q_1) \\ L_1 sin(q_1) \\ 0 \\ 1 \end{array} \right], \textbf{T}^1_0 \; \textbf{x} = \left[ \begin{array}{cccc} cos(q_0) & -sin(q_0) & 0 & L_0 cos(q_0) \\ sin(q_0) & cos(q_0) & 0 & L_0 sin(q_0)\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \; \left[ \begin{array}{c} L_1 cos(q_1) \\ L_1 sin(q_1) \\ 0 \\ 1 \end{array} \right],](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BT%7D%5E1_0+%5C%3B+%5Ctextbf%7Bx%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcccc%7D+cos%28q_0%29+%26+-sin%28q_0%29+%26+0+%26+L_0+cos%28q_0%29+%5C%5C+sin%28q_0%29+%26+cos%28q_0%29+%26+0+%26+L_0+sin%28q_0%29%5C%5C+0+%26+0+%26+1+%26+0+%5C%5C+0+%26+0+%26+0+%26+1+%5Cend%7Barray%7D+%5Cright%5D+%5C%3B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+L_1+cos%28q_1%29+%5C%5C+L_1+sin%28q_1%29+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0)
![\textbf{T}^1_0 \textbf{x} = \left[ \begin{array}{c} L_1 cos(q_0) cos(q_1) - L_1 sin(q_0) sin(q_1) + L_0 cos(q_0) \\ L_1 sin(q_0) cos(q_1) + L_1 cos(q_0) sin(q_1) + L_0 sin(q_0) \\ 0 \\ 1 \end{array} \right] \textbf{T}^1_0 \textbf{x} = \left[ \begin{array}{c} L_1 cos(q_0) cos(q_1) - L_1 sin(q_0) sin(q_1) + L_0 cos(q_0) \\ L_1 sin(q_0) cos(q_1) + L_1 cos(q_0) sin(q_1) + L_0 sin(q_0) \\ 0 \\ 1 \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BT%7D%5E1_0+%5Ctextbf%7Bx%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+L_1+cos%28q_0%29+cos%28q_1%29+-+L_1+sin%28q_0%29+sin%28q_1%29+%2B+L_0+cos%28q_0%29+%5C%5C+L_1+sin%28q_0%29+cos%28q_1%29+%2B+L_1+cos%28q_0%29+sin%28q_1%29+%2B+L_0+sin%28q_0%29+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=555555&s=0) where, by pulling out the
where, by pulling out the  term and using the trig identities
term and using the trig identities
 and
and
 the position of our end-effector can be rewritten:
the position of our end-effector can be rewritten:
![\left[ \begin{array}{c} L_0 cos(q_0) + L_1 cos(q_0 + q_1) \\ L_0 sin(q_0) + L_1 sin(q_0 + q_1) \\ 0 \end{array} \right], \left[ \begin{array}{c} L_0 cos(q_0) + L_1 cos(q_0 + q_1) \\ L_0 sin(q_0) + L_1 sin(q_0 + q_1) \\ 0 \end{array} \right],](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+L_0+cos%28q_0%29+%2B+L_1+cos%28q_0+%2B+q_1%29+%5C%5C+L_0+sin%28q_0%29+%2B+L_1+sin%28q_0+%2B+q_1%29+%5C%5C+0+%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0) which is the position of the end-effector in terms of joint angles. As mentioned above, however, both the position of the end-effector and its orientation are needed; the rotation of the end-effector relative to the base frame must also be defined.
which is the position of the end-effector in terms of joint angles. As mentioned above, however, both the position of the end-effector and its orientation are needed; the rotation of the end-effector relative to the base frame must also be defined.
Accounting for orientation
Fortunately, defining orientation is simple, especially for systems with only revolute and prismatic joints (spherical joints will not be considered here). With prismatic joints, which are linear and move in a single plane, the rotation introduced is 0. With revolute joints, the rotation of the end-effector in each axis is simply a sum of rotations of each joint in their respective axes of rotation.
In the example case, the joints are rotating around the axis, so the rotation part of our end-effector state is
axis, so the rotation part of our end-effector state is
![\left[ \begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ q_0 + q_1 \end{array} \right], \left[ \begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ q_0 + q_1 \end{array} \right],](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Comega_x+%5C%5C+%5Comega_y+%5C%5C+%5Comega_z+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+0+%5C%5C+q_0+%2B+q_1+%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0) where
where 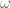 denotes angular rotation. If the first joint had been rotating in a different plane, e.g. in the
denotes angular rotation. If the first joint had been rotating in a different plane, e.g. in the 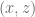 plane around the
plane around the  axis instead, then the orientation would be
axis instead, then the orientation would be
![\left[ \begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array} \right] = \left[ \begin{array}{c} 0 \\ q_0 \\ q_1 \end{array} \right]. \left[ \begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array} \right] = \left[ \begin{array}{c} 0 \\ q_0 \\ q_1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Comega_x+%5C%5C+%5Comega_y+%5C%5C+%5Comega_z+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+q_0+%5C%5C+q_1+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) Partial differentiation
Partial differentiation
Once the position and orientation of the end-effector have been calculated, the partial derivative of these equations need to be calculated with respect to the elements of . For simplicity, the Jacobian will be broken up into two parts,
. For simplicity, the Jacobian will be broken up into two parts, 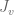 and
and  , representing the linear and angular velocity, respectively, of the end-effector.
, representing the linear and angular velocity, respectively, of the end-effector.
The linear velocity part of our Jacobian is:
![\textbf{J}_v(\textbf{q}) = \left[ \begin{array}{cc} \frac{\partial x}{\partial q_0} & \frac{\partial x}{\partial q_1} \\ \frac{\partial y}{\partial q_0} & \frac{\partial y}{\partial q_1} \\ \frac{\partial z}{\partial q_0} & \frac{\partial z}{\partial q_1} \end{array} \right] = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \\ 0 & 0 \end{array} \right]. \textbf{J}_v(\textbf{q}) = \left[ \begin{array}{cc} \frac{\partial x}{\partial q_0} & \frac{\partial x}{\partial q_1} \\ \frac{\partial y}{\partial q_0} & \frac{\partial y}{\partial q_1} \\ \frac{\partial z}{\partial q_0} & \frac{\partial z}{\partial q_1} \end{array} \right] = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \\ 0 & 0 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BJ%7D_v%28%5Ctextbf%7Bq%7D%29+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+%5Cfrac%7B%5Cpartial+x%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+x%7D%7B%5Cpartial+q_1%7D+%5C%5C+%5Cfrac%7B%5Cpartial+y%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+y%7D%7B%5Cpartial+q_1%7D+%5C%5C+%5Cfrac%7B%5Cpartial+z%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+z%7D%7B%5Cpartial+q_1%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+-L_0+sin%28q_0%29+-+L_1+sin%28q_0+%2B+q_1%29+%26+-+L_1+sin%28q_0+%2B+q_1%29+%5C%5C+L_0+cos%28q_0%29+%2B+L_1+cos%28q_0+%2B+q_1%29+%26+L_1+cos%28q_0+%2B+q_1%29+%5C%5C+0+%26+0+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) The angular velocity part of our Jacobian is:
The angular velocity part of our Jacobian is:
![\textbf{J}_\omega(\textbf{q}) = \left[ \begin{array}{cc} \frac{\partial \omega_x}{\partial q_0} & \frac{\partial \omega_x}{\partial q_1} \\ \frac{\partial \omega_y}{\partial q_0} & \frac{\partial \omega_y}{\partial q_1} \\ \frac{\partial \omega_z}{\partial q_0} & \frac{\partial \omega_z}{\partial q_1} \end{array} \right] = \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right]. \textbf{J}_\omega(\textbf{q}) = \left[ \begin{array}{cc} \frac{\partial \omega_x}{\partial q_0} & \frac{\partial \omega_x}{\partial q_1} \\ \frac{\partial \omega_y}{\partial q_0} & \frac{\partial \omega_y}{\partial q_1} \\ \frac{\partial \omega_z}{\partial q_0} & \frac{\partial \omega_z}{\partial q_1} \end{array} \right] = \left[ \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BJ%7D_%5Comega%28%5Ctextbf%7Bq%7D%29+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+%5Cfrac%7B%5Cpartial+%5Comega_x%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+%5Comega_x%7D%7B%5Cpartial+q_1%7D+%5C%5C+%5Cfrac%7B%5Cpartial+%5Comega_y%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+%5Comega_y%7D%7B%5Cpartial+q_1%7D+%5C%5C+%5Cfrac%7B%5Cpartial+%5Comega_z%7D%7B%5Cpartial+q_0%7D+%26+%5Cfrac%7B%5Cpartial+%5Comega_z%7D%7B%5Cpartial+q_1%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+0+%26+0+%5C%5C+0+%26+0+%5C%5C+1+%26+1+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) The full Jacobian for the end-effector is then:
The full Jacobian for the end-effector is then:
![\textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{c} \textbf{J}_v(\textbf{q}) \\ \textbf{J}_\omega(\textbf{q}) \end{array} \right] = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right]. \textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{c} \textbf{J}_v(\textbf{q}) \\ \textbf{J}_\omega(\textbf{q}) \end{array} \right] = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BJ%7D_%7Bee%7D%28%5Ctextbf%7Bq%7D%29+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Ctextbf%7BJ%7D_v%28%5Ctextbf%7Bq%7D%29+%5C%5C+%5Ctextbf%7BJ%7D_%5Comega%28%5Ctextbf%7Bq%7D%29+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+-L_0+sin%28q_0%29+-+L_1+sin%28q_0+%2B+q_1%29+%26+-+L_1+sin%28q_0+%2B+q_1%29+%5C%5C+L_0+cos%28q_0%29+%2B+L_1+cos%28q_0+%2B+q_1%29+%26+L_1+cos%28q_0+%2B+q_1%29+%5C%5C+0+%26+0+%5C%5C+0+%26+0+%5C%5C+0+%26+0+%5C%5C+1+%26+1+%5Cend%7Barray%7D+%5Cright%5D.+&bg=ffffff&fg=555555&s=0) Analyzing the Jacobian
Analyzing the Jacobian
Once the Jacobian is built, it can be analysed for insight about the relationship between and
and  .
.
For example, there is a large block of zeros in the middle of the Jacobian defined above, along the row corresponding to linear velocity along the axis, and the rows corresponding to the angular velocity around the
axis, and the rows corresponding to the angular velocity around the  and
and  axes. This means that the
axes. This means that the  position, and rotations
position, and rotations  and
and  are not controllable. This can be seen by going back to the first Jacobian equation:
are not controllable. This can be seen by going back to the first Jacobian equation:
 No matter what the values of
No matter what the values of  , it is impossible to affect
, it is impossible to affect  ,
,  , or
, or  , because the corresponding rows during the above multiplication with the Jacobian are
, because the corresponding rows during the above multiplication with the Jacobian are  . These rows of zeros in the Jacobian are referred to as its `null space’. Because these variables can’t be controlled, they will be dropped from both
. These rows of zeros in the Jacobian are referred to as its `null space’. Because these variables can’t be controlled, they will be dropped from both 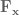 and
and  .
.
Looking at the variables that can be affected it can be seen that given any two of the third can be calculated because the robot only has 2 degrees of freedom (the shoulder and elbow). This means that only two of the end-effector variables can actually be controlled. In the situation of controlling a robot arm, it is most useful to control the
the third can be calculated because the robot only has 2 degrees of freedom (the shoulder and elbow). This means that only two of the end-effector variables can actually be controlled. In the situation of controlling a robot arm, it is most useful to control the  coordinates, so
coordinates, so 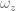 will be dropped from the force vector and Jacobian.
will be dropped from the force vector and Jacobian.
After removing the redundant term, the force vector representing the controllable end-effector forces is
![\textbf{F}_\textbf{x} = \left[ \begin{array}{c}f_x \\ f_y\end{array} \right], \textbf{F}_\textbf{x} = \left[ \begin{array}{c}f_x \\ f_y\end{array} \right],](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BF%7D_%5Ctextbf%7Bx%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7Df_x+%5C%5C+f_y%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0) where
where  is force along the
is force along the  axis,
axis,  is force along the
is force along the  axis, and the Jacobian is written
axis, and the Jacobian is written
![\textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \end{array} \right]. \textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ L_0 cos(q_0) + L_1 cos(q_0 + q_1) & L_1 cos(q_0 + q_1) \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BJ%7D_%7Bee%7D%28%5Ctextbf%7Bq%7D%29+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+-L_0+sin%28q_0%29+-+L_1+sin%28q_0+%2B+q_1%29+%26+-+L_1+sin%28q_0+%2B+q_1%29+%5C%5C+L_0+cos%28q_0%29+%2B+L_1+cos%28q_0+%2B+q_1%29+%26+L_1+cos%28q_0+%2B+q_1%29+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) If instead
If instead  , i.e. torque around the
, i.e. torque around the  axis, were chosen as a controlled force then the force vector and Jacobian would be (assuming force along the
axis, were chosen as a controlled force then the force vector and Jacobian would be (assuming force along the  axis was also chosen):
axis was also chosen):
![\textbf{F}_\textbf{x} = \left[ \begin{array}{c} f_x \\ f_{\omega_z}\end{array} \right], \textbf{F}_\textbf{x} = \left[ \begin{array}{c} f_x \\ f_{\omega_z}\end{array} \right],](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BF%7D_%5Ctextbf%7Bx%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+f_x+%5C%5C+f_%7B%5Comega_z%7D%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0)
![\textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ 1 & 1 \end{array} \right]. \textbf{J}_{ee}(\textbf{q}) = \left[ \begin{array}{cc} -L_0 sin(q_0) - L_1 sin(q_0 + q_1) & - L_1 sin(q_0 + q_1) \\ 1 & 1 \end{array} \right].](https://s0.wp.com/latex.php?latex=%5Ctextbf%7BJ%7D_%7Bee%7D%28%5Ctextbf%7Bq%7D%29+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+-L_0+sin%28q_0%29+-+L_1+sin%28q_0+%2B+q_1%29+%26+-+L_1+sin%28q_0+%2B+q_1%29+%5C%5C+1+%26+1+%5Cend%7Barray%7D+%5Cright%5D.&bg=ffffff&fg=555555&s=0) But we’ll stick with control of the
But we’ll stick with control of the  and
and  forces instead, as it’s a little more straightforward.
forces instead, as it’s a little more straightforward.
Using the Jacobian
With our Jacobian, we can find out what different joint angle velocities will cause in terms of the end-effector linear and angular velocities, and we can also transform desired forces into
forces into 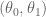 torques. Let’s do a couple of examples. Note that in the former case we’ll be using the full Jacobian, while in the latter case we can use the simplified Jacobian specified just above.
torques. Let’s do a couple of examples. Note that in the former case we’ll be using the full Jacobian, while in the latter case we can use the simplified Jacobian specified just above.
Example 1
Given known joint angle velocities with arm configuration
![\textbf{q} = \left[ \begin{array}{c} \frac{\pi}{4} \\ \frac{3 \pi}{8} \end{array}\right] \;\;\;\; \dot{\textbf{q}} = \left[ \begin{array}{c} \frac{\pi}{10} \\ \frac{\pi}{10} \end{array} \right] \textbf{q} = \left[ \begin{array}{c} \frac{\pi}{4} \\ \frac{3 \pi}{8} \end{array}\right] \;\;\;\; \dot{\textbf{q}} = \left[ \begin{array}{c} \frac{\pi}{10} \\ \frac{\pi}{10} \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Ctextbf%7Bq%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cfrac%7B%5Cpi%7D%7B4%7D+%5C%5C+%5Cfrac%7B3+%5Cpi%7D%7B8%7D+%5Cend%7Barray%7D%5Cright%5D+%5C%3B%5C%3B%5C%3B%5C%3B+%5Cdot%7B%5Ctextbf%7Bq%7D%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cfrac%7B%5Cpi%7D%7B10%7D+%5C%5C+%5Cfrac%7B%5Cpi%7D%7B10%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=555555&s=0) and arm segment lengths
and arm segment lengths  , the
, the  velocities of the end-effector can be calculated by substituting in the system state at the current time into the equation for the Jacobian:
velocities of the end-effector can be calculated by substituting in the system state at the current time into the equation for the Jacobian:

![\dot{\textbf{x}} = \left[ \begin{array}{cc} - sin(\frac{\pi}{4}) - sin(\frac{\pi}{4} + \frac{3\pi}{8}) & - sin(\frac{\pi}{4} + \frac{3\pi}{8}) \\ cos(\frac{\pi}{4}) + cos(\frac{\pi}{4} + \frac{3\pi}{8}) & cos(\frac{\pi}{4} + \frac{3\pi}{8}) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right] \; \left[ \begin{array}{c} \frac{\pi}{10} \\ \frac{\pi}{10} \end{array} \right], \dot{\textbf{x}} = \left[ \begin{array}{cc} - sin(\frac{\pi}{4}) - sin(\frac{\pi}{4} + \frac{3\pi}{8}) & - sin(\frac{\pi}{4} + \frac{3\pi}{8}) \\ cos(\frac{\pi}{4}) + cos(\frac{\pi}{4} + \frac{3\pi}{8}) & cos(\frac{\pi}{4} + \frac{3\pi}{8}) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{array} \right] \; \left[ \begin{array}{c} \frac{\pi}{10} \\ \frac{\pi}{10} \end{array} \right],](https://s0.wp.com/latex.php?latex=%5Cdot%7B%5Ctextbf%7Bx%7D%7D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+-+sin%28%5Cfrac%7B%5Cpi%7D%7B4%7D%29+-+sin%28%5Cfrac%7B%5Cpi%7D%7B4%7D+%2B+%5Cfrac%7B3%5Cpi%7D%7B8%7D%29+%26+-+sin%28%5Cfrac%7B%5Cpi%7D%7B4%7D+%2B+%5Cfrac%7B3%5Cpi%7D%7B8%7D%29+%5C%5C+cos%28%5Cfrac%7B%5Cpi%7D%7B4%7D%29+%2B+cos%28%5Cfrac%7B%5Cpi%7D%7B4%7D+%2B+%5Cfrac%7B3%5Cpi%7D%7B8%7D%29+%26+cos%28%5Cfrac%7B%5Cpi%7D%7B4%7D+%2B+%5Cfrac%7B3%5Cpi%7D%7B8%7D%29+%5C%5C+0+%26+0+%5C%5C+0+%26+0+%5C%5C+0+%26+0+%5C%5C+1+%26+1+%5Cend%7Barray%7D+%5Cright%5D+%5C%3B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cfrac%7B%5Cpi%7D%7B10%7D+%5C%5C+%5Cfrac%7B%5Cpi%7D%7B10%7D+%5Cend%7Barray%7D+%5Cright%5D%2C&bg=ffffff&fg=555555&s=0)
![\dot{\textbf{x}} = \left[ -0.8026, -0.01830, 0, 0, 0, \frac{\pi}{5} \right]^T. \dot{\textbf{x}} = \left[ -0.8026, -0.01830, 0, 0, 0, \frac{\pi}{5} \right]^T.](https://s0.wp.com/latex.php?latex=%5Cdot%7B%5Ctextbf%7Bx%7D%7D+%3D+%5Cleft%5B+-0.8026%2C+-0.01830%2C+0%2C+0%2C+0%2C+%5Cfrac%7B%5Cpi%7D%7B5%7D+%5Cright%5D%5ET.+&bg=ffffff&fg=555555&s=0) And so the end-effector is linear velocity is
And so the end-effector is linear velocity is 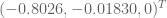 , with angular velocity is
, with angular velocity is  .
.
courtesy;studywolf.
Formally, a Jacobian is a set of partial differential equations:
Why is this important? Well, this goes back to our desire to control in operational (or task) space. We’re interested in planning a trajectory in a different space than the one that we can control directly. Iin our robot arm, control is effected through a set of motors that apply torque to the joint angles, BUT what we’d like is to plan our trajectory in terms of end-effector position (and possibly orientation), generating control signals in terms of forces to apply in
Energy equivalence and Jacobians
Conservation of energy is a property of all physical systems where the amount of energy expended is the same no matter how the system in question is being represented. The planar two-link robot arm shown below will be used for illustration.
Let the joint angle positions be denoted
Work is the application of force over a distance
Power is the rate at which work is performed
Substituting in the equation for work into the equation for power gives:
Building the Jacobian
First, we need to define the relationship between the
The forward transformation matrix
Recall that transformation matrices allow a given point to be transformed between different reference frames. In this case, the position of the end-effector relative to the second joint of the robot arm is known, but where it is relative to the base reference frame (the first joint reference frame in this case) is of interest. This means that only one transformation matrix is needed, transforming from the reference frame attached to the second joint back to the base.
The rotation part of this matrix is straight-forward to define, as in the previous section:
Using this knowledge, the translation part of the transformation matrix is defined:
The point of interest is the end-effector which is defined in reference frame 1 as a function of joint angle,
Accounting for orientation
Fortunately, defining orientation is simple, especially for systems with only revolute and prismatic joints (spherical joints will not be considered here). With prismatic joints, which are linear and move in a single plane, the rotation introduced is 0. With revolute joints, the rotation of the end-effector in each axis is simply a sum of rotations of each joint in their respective axes of rotation.
In the example case, the joints are rotating around the
Once the position and orientation of the end-effector have been calculated, the partial derivative of these equations need to be calculated with respect to the elements of
The linear velocity part of our Jacobian is:
Once the Jacobian is built, it can be analysed for insight about the relationship between
For example, there is a large block of zeros in the middle of the Jacobian defined above, along the row corresponding to linear velocity along the
Looking at the variables that can be affected it can be seen that given any two of
After removing the redundant term, the force vector representing the controllable end-effector forces is
Using the Jacobian
With our Jacobian, we can find out what different joint angle velocities will cause in terms of the end-effector linear and angular velocities, and we can also transform desired
Example 1
Given known joint angle velocities with arm configuration
courtesy;studywolf.

No comments:
Post a Comment